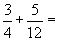Algarismos Romanos
- Nos números de capítulos uma obra.
- Nas cenas de um teatro.
- Nos nomes de papas e imperadores.
- Na designação de congressos, olimpíadas, assembléias...
Regras
A numeração romana utiliza sete letras maiúsculas, que correspondem aos seguintes valores:| Letras | Valores |
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
Se à direita de uma cifra romana se escreve outra igual ou menor, o valor desta se soma ao valor da anterior.
Exemplos:
VI = 6
XXI = 21
LXVII = 67
A letra "I" colocada diante da "V" ou de "X", subtrai uma unidade; a letra "X", precedendo a letra "L" ou a "C", lhes subtrai dez unidades e a letra "C", diante da "D" ou da "M", lhes subtrai cem unidades.
Exemplos:
IV = 4
IX = 9
XL = 40
XC = 90
CD = 400
CM = 900
Em nenhum número se pode pôr uma mesma letra mais de três vezes seguidas. Antigamente se via as vezes a letra "I" ou a "X" até quatro vezes seguidas.
Exemplos:
XIII = 13
XIV = 14
XXXIII = 33
XXXIV = 34
A letra "V", "L" e a "D" não podem se duplicar porque outras letras ("X", "C", "M") representam seu valor duplicado.
Exemplos:
X = 10
C = 100
M = 1.000
Se entre duas cifras quaisquer existe outra menor, o valor desta pertencerá a letra seguinte a ela.
Exemplos:
XIX = 19
LIV = 54
CXXIX = 129
O valor dos números romanos quando multiplicados por mil, colocam-se barras horizontais em cima dos mesmos.
Exemplos:
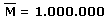
Como se lê uma fração
As frações recebem nomes especiais quando os denominadores são 2, 3, 4, 5, 6, 7, 8, 9 e também quando os denominadores são 10, 100, 1000, ...
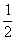 | um meio | 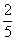 | dois quintos |
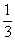 | um terço | 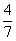 | quatro sétimos |
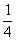 | um quarto | 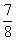 | sete oitavos |
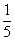 | um quinto | 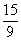 | quinze nonos |
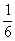 | um sexto | 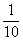 | um décimo |
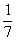 | um sétimo | 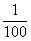 | um centésimo |
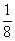 | um oitavo | 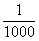 | um milésimo |
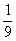 | um nono | 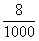 | oito milésimos |
Classificação das frações
Fração própria: o numerador é menor que o denominador: 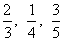
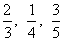
Fração imprópria: o numerador é maior ou igual ao denominador. 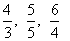
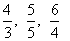
Fração aparente: o numerador é múltiplo do denominador. 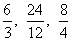
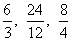

Exercícios de Frações
SÓLIDOS GEOMÉTRICOS - AULA DE MATEMÁTICA

 | Este sólido geométrico chama-se cubo. É um prisma em que todas as faces têm a forma de quadrados. Este sólido geométrico tem: 8 vértices, 12 arestas e 6 faces. |
 | Chamamos paralelepípedo a este prisma. Todas as suas faces têm a forma de rectângulos.Tem 8 vértices, 12 arestas e 6 faces. |
 | Este sólido geométrico é chamado prisma triangular porque as suas bases são triângulos.Tem 6 vértices, 9 arestas, 5 faces e duas bases. |
 | O prisma quadrangular tem nas suas bases quadrados.Tem 8 vértices, 12 aresta, 6 faces e duas bases. |
 | Este sólido chama-se prisma pentagonal, porque as suas bases são pentágonos.Tem 10 vértices, 15 arestas, 7 faces e duas bases. |
 | Este sólido geométrico denomina-se pirâmide triangular porque a sua base é um triângulo.Tem 4 vértices, 6 arestas, 4 faces e 1 base. |
 | Chamamos pirâmide quadrangular a este sólido pois tem um quadrado na sua base.Tem 5 vértices, 8 arestas, 5 faces e 1 base. |
 | A base da pirâmide pentagonal é um pentágono.Tem 6 vértices, 10 arestas, 6 faces e 1 base. |
 | A esfera é um sólido geométrico limitado por uma superfície curva.A sua forma é esférica; não tem bases, não tem vértices e não tem arestas. |
 | Este sólido geométrico chama-se cilindro.Encontra-se limitado por uma superfície curva e tem duas bases com a forma de circunferências |
 | O cone está limitado por uma superfície curva.Tem uma base na forma de circunferência e tem 1 vértice. |
Podemos associar objectos a sólidos geométricos:
 |  |  |  |
| Cone | Cilindro | Esfera | |
 |  |  |
O uso da calculadora e o sistema de numeração
Bloco de ConteúdoMatemática
Conteúdo
Sistema de Numeração Decimal
Conteúdo relacionado
Tudo sobreEssa seqüência didática pode ser proposta quando as crianças já tiverem certo domínio da leitura, escrita e ordem dos números de um, dois e três algarismos.
Objetivos
- Resolver problemas que envolvam a análise do valor do algarismo conforme a posição que ocupa no número.
- Utilizar as propriedades aditivas e multiplicativas do sistema de numeração posicional decimal para resolver problemas que envolvam compor e decompor números em "uns", "dezes" e "cens".
Conteúdos específicos- Reflexão sobre a estrutura aditiva da numeração falada e sua vinculação com as regras da numeração escrita;
- Resolução de problemas que permitam a análise e a formulação de "regras" sobre o valor posicional;
- Início da elaboração de explicações e justificativas sobre a organização do sistema de numeração posicional.
Ano 3º e 4º ano
Tempo estimado
Aproximadamente 8 aulas
Material necessário - "dinheirinho": miniaturas de papel das notas que estão em circulação no país
- calculadoras: uma para cada criança
- cópias de algumas das atividades: uma para cada criança
Desenvolvimento das atividades
1ª etapa - Problemas envolvendo o contexto do uso do dinheiro favorecem a compreensão da idéia de composição e decomposição dos números em "uns", "dezes" e "cens".
Proponha problemas do tipo:
- Tenho 5 notas de 1 real e 2 notas de 10 reais, quanto dinheiro eu tenho?
- Maria possui 3 notas de 100 reais, 4 notas de 10 reais e 3 de 1 real, quanto dinheiro possui?
- Como formar 56 reais com a menor quantidade de notas de 10 e 1 real?
- Como formar 683 reais com a menor quantidade de notas de 100, 10 e 1 real?
Proponha um problema por vez. Você pode organizar a turma ora individualmente, ora em duplas. Circule pela sala enquanto as crianças resolvem os problemas e observe quais procedimentos utilizam. Se notar que alguma criança está com dificuldade para iniciar um procedimento de resolução, ofereça as miniaturas de notas em circulação no país.
Após as crianças resolverem alguns problemas desse tipo, proponha que conversem e observem o que há em comum na forma de resolvê-los. Registre as conclusões das crianças num cartaz para que, em outros momentos, possam consultá-las.
2ª etapa - Antes de propor os problemas previstos nessa segunda etapa será necessário verificar a familiaridade das crianças com a calculadora. Para isso, entregue uma calculadora para cada criança e proponha algumas atividades exploratórias simples como:
- Marquem o 1 na calculadora. Agora, sem apertar nenhuma tecla respondam o que aparecerá se marcarmos o 6? (os alunos podem responder: 61). Agora marquem o 6. O que aconteceu? E se quero escrever 45 (colocar na lousa) qual tecla aperto primeiro?
- Vocês sabem qual é a tecla de mais? (colocar o sinal de + na lousa) E a de igual? (o mesmo procedimento anterior, propor também para os demais sinais)
- Propor algumas operações simples (adições, subtrações, multiplicações e divisões) envolvendo números de um algarismo: 2+3=, 5-4=, 2x2, 8:4,
Problema 1: Ditado de números na calculadora
Organize as crianças em duplas e entregue uma calculadora para cada criança. Dite um número e peça que as crianças o escrevam na calculadora. Depois, pergunte às crianças o que precisarão fazer para que apareça um zero no lugar de um dos algarismos que constituem o número (se você sentir necessidade, pode escrever o número ditado na lousa e o que deverá aparecer no visor da calculadora). Por exemplo:
- Anotem na calculadora o número 459. Sem apagá-lo, pensem que teclas vocês deverão apertar para que apareça o número 409?
Oriente as crianças que não digam a resposta em voz alta e que anotem as teclas que vão apertando para depois poder reconstituir o que fizeram. Enfatizem que não podem apagar o 459.
Em seguida, dite um número parecido, por exemplo, 452 e, sem apagá-lo, transforme-o em 402. Proponha que discutam com a dupla o que será necessário fazer para que ocorra essa transformação. Oriente-as a combinarem quais ordens deverão dar para a calculadora antes de realizar as próximas operações.
Provavelmente nas primeiras situações propostas às crianças operarão por ensaio e erro. Por exemplo, para transformar 459 em 409 primeiro tirarão o 5. Ao conferir no visor o resultado, constatam que o procedimento está errado, pois o número que aparecerá no visor será o 454, e não 409 como solicitado. Dessa forma, podem rever seu procedimento e tentar com outros números, provavelmente experimentarão o 50.
Após cada situação é importante propor a discussão coletiva, perguntando como as crianças se deram conta que deveriam realizar esta operação. Provavelmente, os argumentos das crianças estarão baseados exclusivamente na numeração falada, por exemplo: “Era quatrocentos e cinqüenta e nove. Então, tirei o cinqüenta”.
Problema 2Mantenha o mesmo tipo de proposta do problema anterior, variando os números. Alterne a grandeza numérica (números de dois, três e quatro algarismos) e o lugar onde deverá aparecer o zero (na unidade, na dezena, na centena). Por exemplo:
Anote na calculadora os números da primeira coluna (um por vez) e, sem apagá-lo, transforme-o no número da segunda coluna:
- Transforme 34 em 30
- Transforme 432 em 402
- Transforme 9354 em 9054
- Transforme 345 em 305
- Transforme 9815 em 9015
- Transforme 9268 em 9208
- Transforme 6275 em 6075
- Transforme 7403 em 7003
Circule pela sala e anote alguns comentários das crianças e formas utilizadas para resolver o problema para retomar em outro momento.
Observação: não é recomendável registrar o número com ponto, separando a unidade de mil, pois pode confundir as crianças na hora de registrá-lo na calculadora.
3ª etapa - Explicando as aprendizagens das aulas anteriores
Atividade 1
Inicie a atividade conversando com as crianças sobre o que fizeram nas aulas: “Lembra do que fizemos nas últimas aulas? Anotei algumas coisas interessantes que fizeram...”
Retome algumas das situações propostas. Por exemplo: transformar 34 em 30.
Peça que as crianças expliquem o que foi preciso fazer para conseguir essas transformações. Anote as explicações num cartaz para que possam retomar posteriormente.
Retome o segundo caso, por exemplo, transformar 452 em 402. "E neste caso, o que descobriram?"
Se for necessário proponha outros cálculos desse tipo.
Atividade 2
Organize as conclusões das crianças numa folha (veja exemplo a seguir). Organize a turma em duplas, entregue uma cópia das suas anotações para cada criança e proponha que analisem como resolveram os problemas propostos nas aulas anteriores e procurem explicá-los.
"Vocês fizeram vários problemas em que eu ditei um número para que escrevessem na calculadora. Depois, eu pedia que fizessem algo para que aparecesse um zero no lugar de um dos algarismos do número. Lembram? Agora, vocês vão se juntar a um colega e explicar alguns cálculos que vocês fizeram."
- Para transformar 136 em 130 vocês fizeram 136 - 6 = . Como fizeram para saber que deveriam tirar 6 e não 60 ou 600?
- Para transformar 149 em 109 vocês fizeram 149 – 40 = . Como fizeram para saber que deveriam tirar 40 e não 4 ou 400?
- Para transformar 6275 em 6075 vocês fizeram 6275 – 200 = . Como fizeram para saber que deveriam tirar 200 e não 2 ou 20?
Colocar na lousa os cálculos que as crianças fizeram nas aulas anteriores e orientá-los para que procurem explicar oralmente, conversando com o colega. Nesse momento, não é necessário escrever;
A professora (formadora) circula pela classe acompanhando as duplas e ajudando-as a formular suas explicações;
Organizar a discussão coletiva. Discutir cada caso. Propor que uma dupla explique o primeiro cálculo. A professora do grupo, Lilian, vai anotando o que as crianças vão dizendo para depois poder recuperar (futuramente, poderá anotar essas conclusões num cartaz para que as crianças copiem em seus cadernos);
Depois que concluírem o primeiro cálculo, propor que outra dupla explique o segundo e por fim o terceiro.
Oriente-os a conversarem com o colega procurando explicar o que fizeram nas aulas anteriores, nesse momento não é necessário escrever. Circule pela sala acompanhando as duplas, ajudando-as a formular suas explicações.
Depois, organize a discussão coletiva. Coloque em discussão cada um dos casos selecionados por você e peça que as crianças digam a que conclusões chegaram (peça que uma das duplas comece compartilhando com o grupo sua conversa e depois pergunte a opinião de outra dupla. Quando concluírem o primeiro tipo de cálculo, passe para o segundo e assim por diante). Anote (ou grave) as observações das crianças, posteriormente você pode anotá-las num cartaz e propor que as crianças as copiem em seus cadernos.
4ª etapa – Calculadora quebrada
Atividade 1
Proponha que as crianças façam aparecer no visor da calculadora os números listados abaixo, mas agora sem digitar o número 2. Oriente-os para anotar ao lado de cada número as teclas que digitou para obtê-lo. Leia o problema para as crianças e, em seguida, converse sobre o preenchimento da tabela, indicando o local onde devem anotar as teclas que utilizaram.
Observação: você pode "contar uma historinha" para as crianças, dizendo, por exemplo, que quebrou determinada tecla da calculadora...
| Números | Teclas utilizadas |
| 152 | 100 + 53 - 1= (por exemplo) |
| 28 | |
| 214 |
Após terminarem de preencher a tabela reúna-os em grupos e proponha que comparem os passos que seguiram para obter os números desejados.
Atividade 2Em outra aula, proponha novamente que digitem alguns números sem utilizar determinada tecla da calculadora, mas desta vez fazendo o menor número de operações possível.
Desta vez a tecla 5 está quebrada... Faça aparecer os números listados abaixo no visor da sua calculadora fazendo o mínimo de operações possível. Não esqueça de anotar na coluna ao lado de cada número as teclas que você digitou.
| Números | Teclas utilizadas |
| 35 | 38 - 3 = (por exemplo) |
| 157 | |
| 532 |
Após terem preenchido a tabela, proponha que comparem e analisem os passos que seguiram. Anote suas conclusões num cartaz que será afixado na parede da sala de aula.
Quer saber mais?5ª etapa: Avaliação Retome as anotações que fizeram referentes aos problemas propostos na 2ª etapa dessa seqüência. Desta vez você irá ditar números para as crianças compostos pelos mesmos algarismos, por exemplo, 33, 222, 4444, 7777.
Alterne o lugar em que o zero deverá aparecer, por exemplo: "Anote na calculadora quatro mil quatrocentos e quarenta e quatro. Agora, sem apagar, transforme-o em quatro mil e quarenta e quatro."
"Agora digite quatro mil quatrocentos e quarenta e quatro e sem apagá-lo transforme-o em quatro mil quatrocentos e quatro."
Peça para as crianças explicarem como fizeram para saber que ordens dar a calculadora.
Você pode propor também outros problemas que envolvam outro tipo de transformação nos números: Anotar o 66 no visor da calculadora. Com uma soma fazer com que apareça o 666, depois o 766 e em seguida o 866.
BIBLIOGRAFIA
• Didática da Matemática, org. Cecília Parra e Irmã Saiz, editora Artmed
• Projeto Matemática É D+, Fundação Victor Civita
• Diseño Curricular para la Educación Primaria. Primer Ciclo Volúmen 1 / Dirección General de Cultura y Educación - 1a ed. - La Plata: Dir. General de Cultura y Educación de la Provincia de Buenos Aires, 2008:
http://abc.gov.ar/lainstitucion/sistemaeducativo/educprimaria/default.cfm• “Plan Plurianual para el Mejoramiento de la enseñanza - Cálculo mental con números naturales – Docente” - Governo da Cidade de Buenos Aires, Secretaria de Educação, Direção Geral de Planejamento. Coordenação autoral: Patricia Sadovsky. Elaboração do material: María Emilia Quaranta, Héctor Ponce:
http://www.buenosaires.gov.ar/areas/educacion/curricula/plan_pluri.php
• Didática da Matemática, org. Cecília Parra e Irmã Saiz, editora Artmed
• Projeto Matemática É D+, Fundação Victor Civita
• Diseño Curricular para la Educación Primaria. Primer Ciclo Volúmen 1 / Dirección General de Cultura y Educación - 1a ed. - La Plata: Dir. General de Cultura y Educación de la Provincia de Buenos Aires, 2008:
http://abc.gov.ar/lainstitucion/sistemaeducativo/educprimaria/default.cfm• “Plan Plurianual para el Mejoramiento de la enseñanza - Cálculo mental con números naturales – Docente” - Governo da Cidade de Buenos Aires, Secretaria de Educação, Direção Geral de Planejamento. Coordenação autoral: Patricia Sadovsky. Elaboração do material: María Emilia Quaranta, Héctor Ponce:
http://www.buenosaires.gov.ar/areas/educacion/curricula/plan_pluri.php
Consultoria: Priscila Monteiro
Pedagoga e professora de Matemática, formadora do projeto Matemática É D+, da Fundação Victor Civita.
http://revistaescola.abril.com.br/matematica/pratica-pedagogica/uso-calculadora-sistema-numeracao-429064.shtmlPedagoga e professora de Matemática, formadora do projeto Matemática É D+, da Fundação Victor Civita.
Introdução ao estudo de gráficos
Bloco de ConteúdoTratamento da informação
Conteúdo
Tratamento da informação
Mais sobre tratamento da informação
Reportagens- Estatísticas bem trabalhadas
- Relato de Daniela Mazoco, Professora Nota 10 de 2009
- Alfabetização estatística
- Problemas matemáticos sem problemas
Planos de aula
Interpretar e transmitir informações por meio de gráficos; utilizando a escala para dar precisão
Conteúdo
Gráficos de barras
Anos
1º ao 3º ano
Tempo estimado
Três aulas
Material necessário
Jornais e revistas em que apareçam diferentes tipos de gráfico, papel quadriculado, régua.
Desenvolvimento
1ª etapa
Proponha à turma uma pesquisa sobre gráficos em jornais e revistas. Divida os alunos em grupos de quatro e distribua, para cada um, materiais que contenham vários tipos de gráfico – barras, linhas, pizza etc. Certifique-se que os gráficos escolhidos tratem de temas que os alunos tem familiaridade - número de alunos na escola, dados sobre desmatamento, população etc. Coloque no quadro algumas perguntas:
- Que tipo de informação cada gráfico apresenta?
- Qual deles vocês julgam mais fácil de ler? Por quê?
Peça que registrem as informações no caderno e, em seguida, abra a discussão sobre as características e a adequação de cada formato às informações nele contidas. Peça que os alunos elejam o formato que lhes parece mais fácil. É bem provável que sejam escolhidos os gráficos de barras verticais.
2ª etapa
Selecione alguns gráficos de barras para uma análise detalhada. Procure representações que tragam diferentes escalas e intervalos - um gráfico pode ter uma escala de zero a dez e marcações de dois e dois, outro pode variar de zero a cem, com intervalos de dez em dez, e assim por diante.
Comece perguntando aos alunos quais são as principais informações apresentadas. O que mostra cada gráfico? Do que se trata?
Em seguida, chame a atenção da turma para as diferentes escalas e intervalos utilizados. Todas as representações usam a mesma escala? Não? Por quê? Explique aos alunos que, na hora de criar um gráfico, é preciso pensar em uma escala em que caibam todas as informações que queremos. Se os dados que vamos inserir variam de zero a dez, o gráfico deve ter, pelo menos, uma escala com esses valores.
Peça que observem, também, os intervalos em que os gráficos estão divididos. Explique à turma que essa divisão ajuda a tornar o gráfico mais preciso e claro. Os alunos vão perceber que são intervalos regulares e crescentes: 2, 4, 6, 8... 5, 10, 15, 20... Proponha que respondam oralmente: Se eu fizer um gráfico com intervalos de três em três, quais números devo incluir? A classe certamente dirá 3, 6, 9, 12...
3ª etapa
Proponha que a turma faça uma pesquisa de opinião na escola. Comece explicando aos alunos que a atividade consiste em um levantamento de informações sobre um tema determinado. Para isso, é preciso escolher um assunto, formular perguntas e conversar com os entrevistados.
Em seguida, escolha o tema da pesquisa com a turma. Uma opção é fazer um levantamento sobre os livros lidos na roda de leitura da última semana, perguntando aos colegas das outras classes qual obra mais gostaram. O resultado pode ser usado para que os alunos preparem, na aula de Língua Portuguesa, uma resenha sobre o livro mais votado.
Divida a turma em grupos de quatro e proponha que entrevistem os colegas das outras classes. Explique que cada grupo deve levar um caderno com uma tabela, em que as respostas serão colocadas:

4ª etapa
De volta à sala, proponha que a turma socialize as informações e coloque-as em uma tabela coletiva. Em seguida, peça que os grupos se reúnem e somem os resultados. No exemplo dos livros, eles descobrirão que 22 colegas gostam do primeiro, 16 do segundo, 14 do terceiro etc.

Em seguida, peça que cada grupo elabore um gráfico de barras para expressar os resultados obtidos. Para isso, retome as explicações da aula anterior. Mostre a eles que, em primeiro lugar, é preciso traçar os eixos X e Y no papel quadriculado com a ajuda da régua. Em seguida, cada grupo deve definir a escala e os intervalos que lhes parecerem mais eficientes para apresentar os dados. É provável que surjam opções diferentes, o que irá enriquecer a discussão dos resultados.

Dê um tempo para que os grupos terminem e faça uma exposição dos resultados obtidos. Discuta com a turma as diferentes escalas e intervalos usados. Quais foram mais adequados? Por quê? No exemplo dos livros a melhor opção seria colocar uma escala de zero a 25, dividida de 5 em 5. Pergunte o que aconteceria se os números fossem maiores, com três ou quatro casas decimais. A escala teria que mudar? E os intervalos?
Avaliação
Proponha à turma um novo exercício, com base nos conhecimentos adquiridos na aula. Peça que criem um gráfico com as informações sobre o crescimento populacional da cidade nos últimos cinco anos. Apresente os dados e peça que criem os gráficos individualmente no papel quadriculado. Analise os resultados e certifique-se de que os alunos entenderam como transmitir informações por meio de gráficos e se utilizaram escala e intervalos pertinentes.
Adaptado do texto "Ensinando competências: interpretação e elaboração de gráficos", de Daniela Padovan
Publicado na Revista de Educação - Matemática - Ano 11, Nº 3
http://revistaescola.abril.com.br/matematica/pratica-pedagogica/introducao-ao-estudo-graficos-556512.shtml
Matemática
Conteúdo
Tratamento da Informação
Objetivos
• Refletir sobre as regras do sistema de numeração decimal e apoiar-se nelas para comparar números de diferentes quantidades de algarismos.
• Interpretar informações organizadas em tabelas de dupla entrada.
Conteúdos
• Leitura, comparação e ordenação de números.
• Identificação de regularidades.
Anos
3º e 4º.
Tempo estimado
Um bimestre.
Material necessário
Cartaz com a tabela de dados de casos de dengue no Brasil.
Desenvolvimento
1ª etapa
Confeccione a tabela abaixo em papel craft ou cartolina e fixe-a num local visível na classe.
Providencie cópias menores para cada dupla de alunos com as seguintes perguntas:
1. Qual o estado com o maior número de casos em 2000. E em 2001?
2. Qual o estado com o menor número de casos em 2000? E em 2001?
3. Quais estados tiveram uma redução de dengue de 2000 para 2001? Proponha a troca de pares para que todos comparem e justifiquem as respostas.
2ª etapa
Evite dar a resposta certa de imediato.
O ideal é que as crianças discutam entre elas e comparem em discussões coletivas os critérios utilizados para decidir qual é o número maior.
Avaliação
Anote no cartaz da sala as conclusões dos alunos para problematizá-las. Proponha outras atividades como essa, com dados diferentes.
Planos de aula
Suponhamos que você, professor de Matemática, chegou ao ponto do currículo em que precisa ensinar quantos mililitros cabem em 1 litro. Qual estratégia é a mais eficaz: anotar no quadro a equivalência "1 l = 1.000 ml" e pedir que os alunos a memorizem? Ou levá-los a perceber qual é a relação entre as unidades por meio de uma atividade que envolva, digamos, copos de 250 militros e uma jarra de 1 litro? Nunca é demais lembrar que a melhor alternativa é aquela em que o aluno tem a oportunidade de testar hipóteses para construir o conhecimento. Só mostrar as regras sem considerar o raciocínio que levou à sua construção não ajuda a aplicar o que foi aprendido em outras situações.
Foi pensando na necessidade de mostrar como o conhecimento pode ser generalizado que a professora Elaine Terezinha Mattioli Coviello, da EE Joaquim de Abreu Sampaio Vidal, em Pirangi, a 390 quilômetros de São Paulo, desenvolveu uma sequência didática sobre grandezas e medidas para alunos de 3ª série (leia o quadro abaixo). Baseando-se em problemas concretos, relacionados ao consumo de água, ela envolveu a turma em atividades que exigiam a comparação das unidades de medidas mais usuais - comprimento (metros, centímetros e quilômetros), massa (gramas e quilogramas) e capacidade (mililitros e litros) - e a análise de diversos procedimentos de cálculo - área, perímetro e vazão.
O projeto, que mobilizou a classe e rendeu avanços no aprendizado do conteúdo, foi um dos vencedores do Prêmio Victor Civita - Educador Nota 10. "O trabalho indica que é interessante abordar um problema específico e depois propor outros usos para ampliar a abrangência do que foi aprendido", explica Priscila Monteiro, coordenadora da formação em Matemática da prefeitura de São Caetano do Sul, na Grande São Paulo, e formadora do projeto Matemática É D+, da Fundação Victor Civita. "Nesse sentido, ele pode ser replicado em outras salas de aula por todo o Brasil."
 Elaine Terezinha Mattioli Coviello nasceu em Vista Alegre do Alto, a 385 quilômetros de São Paulo. Casada e mãe de um filho, é docente há 20 anos. Formada em Pedagogia, atua como professora polivalente na EE Joaquim de Abreu Sampaio Vidal, mas aprofundou-se em matemática depois de cursar uma especialização na área. "Os conhecimentos que aprendi no curso e apliquei em minha prática certamente me ajudaram a conceber o projeto premiado", afirma.
Elaine Terezinha Mattioli Coviello nasceu em Vista Alegre do Alto, a 385 quilômetros de São Paulo. Casada e mãe de um filho, é docente há 20 anos. Formada em Pedagogia, atua como professora polivalente na EE Joaquim de Abreu Sampaio Vidal, mas aprofundou-se em matemática depois de cursar uma especialização na área. "Os conhecimentos que aprendi no curso e apliquei em minha prática certamente me ajudaram a conceber o projeto premiado", afirma.
Objetivo
A meta principal era fazer com que as crianças, em vez de apenas montar algoritmos e aplicar fórmulas sem compreender a questão, resolvessem problemas de grandezas e medidas entendendo o porquê dos cálculos. Um desafio impulsionou a investigação da turma de 3ª série: "Quanta água gastamos para lavar o pátio da escola?"
Passo-a-passo
Na primeira etapa, Elaine propôs que as crianças comparassem a quantidade de água presente em diversos recipientes, com e sem graduação de mililitros, e percebessem as relações de equivalência existentes entre eles. Na fase seguinte, incentivou que a turma usasse o mesmo processo para entender outras unidades de medida, como as de tempo e as de comprimento. O terceiro passo já envolvia cálculos que juntavam duas grandezas diferentes. Com relógio, baldes, mangueiras e canecas graduadas, os estudantes anotaram quanta água era despejada durante um minuto. Também aprenderam que, para encontrar a quantidade de litros acumulados em 3 minutos, precisariam multiplicar o valor encontrado por 3. Por fim, aplicaram os conhecimentos para avaliar a forma mais econômica de lavar o pátio. Enquanto um grupo media a quantidade de água usada com uma mangueira para lavar uma área de 4 metros quadrados, outro usava a mesma estratégia para aferir o gasto de água em baldes em uma área semelhante. No fim, todos perceberam que gastam mais com a mangueira, o que significa desperdício, e puderam mudar o comportamento no uso da água na escola e em casa.
Avaliação
Elaine acompanhou o desempenho de cada aluno tendo em mãos vários registros, o que permitiu a mudança de rumos nas propostas e a retomada de temas pouco compreendidos. Ao fim de cada etapa, as crianças produziram textos que formaram portfólios, cartazes que resumiram o aprendido, e gráficos construídos no computador para organizar os novos conhecimentos.Copos, calendários e metros para apresentar as medidas
Para a turma entender que é possível usar uma situação particular de estudo para generalizar e extrapolar o mesmo raciocínio para outros casos, a intervenção do professor é essencial (leia a sequência didática). No bloco de conteúdo de grandezas e medidas, para introduzir o conceito de equivalência, por exemplo, uma opção é pedir que os estudantes levem diversos tipos de recipiente: copos de lanchonete, potinhos de supermercado, vasilhames com graduação de mililitros, baldes grandes e garrafas de refrigerante. Medir quantas garrafas cabem em um balde já permite a primeira aproximação com a ideia de comparação de capacidades. A familiaridade aumenta se a garrafa tiver, por exemplo, um rótulo que indique o conteúdo que suporta: a garotada descobre que é preciso examinar bem os recipientes para encontrar informações que possibilitem a comparação numérica.
O mesmo processo vale para apresentar as unidades de tempo: trabalhar o uso do calendário e ensinar a ver horas são maneiras de entender as equivalências entre minutos, horas e segundos. Entre as atividades possíveis estão, por exemplo, localizar datas importantes dentro de um mês específico e calcular quanto tempo falta para chegar lá.
Já para pensar nas medidas de comprimento, o professor contrapõe formas de estimar as distâncias até a escola. Enquanto um aluno pode ter a noção de que percorre 1 quilômetro, outro diz que são dez quadras, enquanto um terceiro dá a resposta em metros. Essa pode ser uma excelente ocasião para explicar a diferença entre medidas convencionais (nesse caso, metros ou quilômetros) e não convencionais (quadras).
Mais que apenas fórmulas, a generalização exige desafios
A partir desse ponto, você já pode estimular o desenvolvimento de outra competência bastante importante: identificar qual medida utilizar para estimar uma grandeza. Será quilograma? Metro? Litro? Minutos? Mostre que a resposta depende do que se deseja medir - massa, comprimento (ou cálculos como área e distância), volume ou tempo. Para cada uma dessas características, existe um instrumento adequado. É essencial deixar isso claro porque nem sempre é evidente para as crianças dessa faixa etária a maneira de usar cada instrumento de medida. Por outras palavras, não se trata apenas de saber que a quantidade de líquido se mede em litros, mas também que medir a capacidade de uma caixa- d’água, por exemplo, com baldes e não com xícaras, vai deixar o cálculo menos trabalhoso, embora menos preciso.
Finalmente, chega a hora de generalizar a explicação, trazendo para um contexto mais amplo os exemplos particulares. Nesse ponto, é importante, sim, mostrar as relações de equivalência (coisas como 1 l = 1.000 ml, para voltar ao exemplo do início do texto) e os algoritmos que colocam as unidades em relação, caso das regras para o cálculo de área, perímetro, volume e vazão. Mas o que se espera, pelo próprio caminho de pesquisa propiciado pela sequência didática, é que esse conhecimento faça sentido e não seja apenas mais uma frase para decorar. A tarefa, agora, é abastecer a turma com novas situações problema para aplicar as fórmulas, mostrando sua vantagem principal: facilitar o cálculo, levando ao resultado correto independentemente dos números envolvidos e da questão proposta.
Como último lembrete, vale dizer que, nesse percurso do particular ao geral, é preciso ficar atento para não cair na armadilha de que tudo que se ensina precisa ser aplicável no cotidiano. A verdade é que o conhecimento matemático não pode ser reduzido meramente a fins instrumentais - conteúdos como números primos e equações de 2º grau têm, em tese, pouca relação com a realidade concreta. Nem por isso devem ser abandonados: ao contrário, são essenciais ao desenvolvimento do pensamento matemático e lógico. Mas o caminho para trabalhar tanto as questões ligadas ao dia-a-dia como as abstratas é o mesmo: desafiar o aluno com situações problema, deixando-o pensar e encaminhando seu raciocínio de modo que ele possa encontrar a melhor solução.
Publicado na Revista de Educação - Matemática - Ano 11, Nº 3
http://revistaescola.abril.com.br/matematica/pratica-pedagogica/introducao-ao-estudo-graficos-556512.shtml
De olho na dengue
Bloco de ConteúdoMatemática
Conteúdo
Tratamento da Informação
Conteúdo relacionado
Tudo sobre• Refletir sobre as regras do sistema de numeração decimal e apoiar-se nelas para comparar números de diferentes quantidades de algarismos.
• Interpretar informações organizadas em tabelas de dupla entrada.
Conteúdos
• Leitura, comparação e ordenação de números.
• Identificação de regularidades.
Anos
3º e 4º.
Tempo estimado
Um bimestre.
Material necessário
Cartaz com a tabela de dados de casos de dengue no Brasil.
Desenvolvimento
1ª etapa
Confeccione a tabela abaixo em papel craft ou cartolina e fixe-a num local visível na classe.
| Distribuição de casos de dengue por estado em 2000 e 2001 | ||
| Estado | 2000 | 2001 |
| Rio de Janeiro | 4.281 | 68.438 |
| São Paulo | 15.445 | 51.177 |
| Roraima | 7.295 | 5.166 |
| Distrito Federal | 1.030 | 2.895 |
| Rondônia | 3.635 | 1.652 |
| Fonte Fundação Nacional de Saúde | ||
Providencie cópias menores para cada dupla de alunos com as seguintes perguntas:
1. Qual o estado com o maior número de casos em 2000. E em 2001?
2. Qual o estado com o menor número de casos em 2000? E em 2001?
3. Quais estados tiveram uma redução de dengue de 2000 para 2001? Proponha a troca de pares para que todos comparem e justifiquem as respostas.
2ª etapa
Evite dar a resposta certa de imediato.
O ideal é que as crianças discutam entre elas e comparem em discussões coletivas os critérios utilizados para decidir qual é o número maior.
Avaliação
Anote no cartaz da sala as conclusões dos alunos para problematizá-las. Proponha outras atividades como essa, com dados diferentes.
Solução na medida
Desafios reais com unidades de comprimento, massa, capacidade e tempo colaboram para explicar equivalências e relações entre grandezas
Beatriz Santomauro mailto:bsantomauro@abril.com.br, de Pirangi, SP
ENTENDENDO A VAZÃO Na EE Joaquim
de Abreu Sampaio Vidal, a turma percebe
a ligação entre tempo e capacidade
Fotos: Marcos Rosa. Clique para ampliar
de Abreu Sampaio Vidal, a turma percebe
a ligação entre tempo e capacidade
Fotos: Marcos Rosa. Clique para ampliar
Conteúdo relacionado
Vídeos- O trabalho da Educadora Nota 10
- Matemática é D+ - Medidas de uma toalha
- Matemática é D+ - Unidades de medida
Planos de aula
- Relações entre unidades
- Pesos e volumes
- Metro, quilômetro. Litro, mililitro
- Aproximação e estimativa
Foi pensando na necessidade de mostrar como o conhecimento pode ser generalizado que a professora Elaine Terezinha Mattioli Coviello, da EE Joaquim de Abreu Sampaio Vidal, em Pirangi, a 390 quilômetros de São Paulo, desenvolveu uma sequência didática sobre grandezas e medidas para alunos de 3ª série (leia o quadro abaixo). Baseando-se em problemas concretos, relacionados ao consumo de água, ela envolveu a turma em atividades que exigiam a comparação das unidades de medidas mais usuais - comprimento (metros, centímetros e quilômetros), massa (gramas e quilogramas) e capacidade (mililitros e litros) - e a análise de diversos procedimentos de cálculo - área, perímetro e vazão.
O projeto, que mobilizou a classe e rendeu avanços no aprendizado do conteúdo, foi um dos vencedores do Prêmio Victor Civita - Educador Nota 10. "O trabalho indica que é interessante abordar um problema específico e depois propor outros usos para ampliar a abrangência do que foi aprendido", explica Priscila Monteiro, coordenadora da formação em Matemática da prefeitura de São Caetano do Sul, na Grande São Paulo, e formadora do projeto Matemática É D+, da Fundação Victor Civita. "Nesse sentido, ele pode ser replicado em outras salas de aula por todo o Brasil."
Um projeto que não fez água

POLIVALENTE ESPECIAL Com o curso de especialização em Matemática, Elaine mudou a prática em aula
Objetivo
A meta principal era fazer com que as crianças, em vez de apenas montar algoritmos e aplicar fórmulas sem compreender a questão, resolvessem problemas de grandezas e medidas entendendo o porquê dos cálculos. Um desafio impulsionou a investigação da turma de 3ª série: "Quanta água gastamos para lavar o pátio da escola?"
Passo-a-passo
Na primeira etapa, Elaine propôs que as crianças comparassem a quantidade de água presente em diversos recipientes, com e sem graduação de mililitros, e percebessem as relações de equivalência existentes entre eles. Na fase seguinte, incentivou que a turma usasse o mesmo processo para entender outras unidades de medida, como as de tempo e as de comprimento. O terceiro passo já envolvia cálculos que juntavam duas grandezas diferentes. Com relógio, baldes, mangueiras e canecas graduadas, os estudantes anotaram quanta água era despejada durante um minuto. Também aprenderam que, para encontrar a quantidade de litros acumulados em 3 minutos, precisariam multiplicar o valor encontrado por 3. Por fim, aplicaram os conhecimentos para avaliar a forma mais econômica de lavar o pátio. Enquanto um grupo media a quantidade de água usada com uma mangueira para lavar uma área de 4 metros quadrados, outro usava a mesma estratégia para aferir o gasto de água em baldes em uma área semelhante. No fim, todos perceberam que gastam mais com a mangueira, o que significa desperdício, e puderam mudar o comportamento no uso da água na escola e em casa.
Avaliação
Elaine acompanhou o desempenho de cada aluno tendo em mãos vários registros, o que permitiu a mudança de rumos nas propostas e a retomada de temas pouco compreendidos. Ao fim de cada etapa, as crianças produziram textos que formaram portfólios, cartazes que resumiram o aprendido, e gráficos construídos no computador para organizar os novos conhecimentos.
VER A EQUIVALÊNCIA Ao completar os copos com água, os alunos notam a relação entre os diferentes recipientes. Clique para ampliar
O mesmo processo vale para apresentar as unidades de tempo: trabalhar o uso do calendário e ensinar a ver horas são maneiras de entender as equivalências entre minutos, horas e segundos. Entre as atividades possíveis estão, por exemplo, localizar datas importantes dentro de um mês específico e calcular quanto tempo falta para chegar lá.
Já para pensar nas medidas de comprimento, o professor contrapõe formas de estimar as distâncias até a escola. Enquanto um aluno pode ter a noção de que percorre 1 quilômetro, outro diz que são dez quadras, enquanto um terceiro dá a resposta em metros. Essa pode ser uma excelente ocasião para explicar a diferença entre medidas convencionais (nesse caso, metros ou quilômetros) e não convencionais (quadras).
Mais que apenas fórmulas, a generalização exige desafios
REGISTRO DIGITAL Em programas de computador, a turma construiu gráficos das grandezas medidas. Clique para ampliar
Finalmente, chega a hora de generalizar a explicação, trazendo para um contexto mais amplo os exemplos particulares. Nesse ponto, é importante, sim, mostrar as relações de equivalência (coisas como 1 l = 1.000 ml, para voltar ao exemplo do início do texto) e os algoritmos que colocam as unidades em relação, caso das regras para o cálculo de área, perímetro, volume e vazão. Mas o que se espera, pelo próprio caminho de pesquisa propiciado pela sequência didática, é que esse conhecimento faça sentido e não seja apenas mais uma frase para decorar. A tarefa, agora, é abastecer a turma com novas situações problema para aplicar as fórmulas, mostrando sua vantagem principal: facilitar o cálculo, levando ao resultado correto independentemente dos números envolvidos e da questão proposta.
ECONOMIA CALCULADA A comparação da água usada para lavar o pátio revelou que a mangueira gasta mais que o balde. Clique para ampliar
Quer saber mais?
CONTATOS
EE Joaquim de Abreu Sampaio Vidal, R. Prudente de Moraes, 993, 15820-000, Pirangi, SP, tel. (17) 3386-3332
Elaine Terezinha Mattioli Coviello
BIBLIOGRAFIA
Introdução ao Estudo das Situações Didáticas - Conteúdos e Métodos de Ensino, Guy Brousseau, 128 págs., Ed. Ática, tel. 0800-115-152, 32,90 reais
INTERNET
Sequências didáticas sobre grandezas e medidas (em espanhol)
EE Joaquim de Abreu Sampaio Vidal, R. Prudente de Moraes, 993, 15820-000, Pirangi, SP, tel. (17) 3386-3332
Elaine Terezinha Mattioli Coviello
BIBLIOGRAFIA
Introdução ao Estudo das Situações Didáticas - Conteúdos e Métodos de Ensino, Guy Brousseau, 128 págs., Ed. Ática, tel. 0800-115-152, 32,90 reais
INTERNET
Sequências didáticas sobre grandezas e medidas (em espanhol)
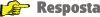
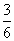 da pizza
da pizza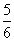 da pizza
da pizza do que eu tenho são 195 reais, a quanto corresponde
do que eu tenho são 195 reais, a quanto corresponde 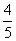 do que eu tenho?
do que eu tenho?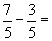 b)
b) 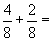 c)
c)